jaehwi

I am an amazing person!

10 분 소요

1. Introduction

보통 데이터분석가들은 새로운 Image dataset을 만났을 때, 이게 얼마나 어려운 문제인지 파악하고 싶어합니다.

  1. 어떤 클래스가 가장 분류하기 힘든지?
  2. CNN 학습을 위해 필요한 최소의 data size는 무엇인지?

그러나 그런 측정이 가능한 표준 framework가 아직은 없습니다. 그래서 현재는 여러가지 CNN 모형들을 만들고, 학습한 뒤, test set에서의 결과들을 비교해서 그러한 정보들을 얻어냅니다. 그러나 이 방법은 두 가지 문제점이 있습니다.

  1. 시간이 너무 많이 소요되고,
  2. fully-annotated dataset이 필요합니다.

그래서 classification problem의 complexity를 측정하기 위해, dataset 단계에서 난이도를 평가할 수 있는 c-measures를 고안했습니다. c-measure의 목표는 얼마나 class들이 entangled 돼있는지를 평가하는 것이며, class들이 feature-space에서 많이 겹쳐있을 수록 분류하기 어렵다고 가정합니다.

하지만, 현존하는 c-measures는 large-image dataset에 적합하지 않습니다.

  • original feature space에서 separable 가능하다고 가정하거나,
  • 오직 two-class problems만을 고려하기도 합니다.
  • 아니면, 샘플 수 and/or feature 수 만큼의 차원 연산이 필요해 너무 느리거나 memory를 너무 소비합니다.
  • raw 데이터에서만 작동하는 c-measures도 적합하지 않습니다. 왜냐하면 요즘 CNN은 feature space로 projection해서 데이터를 분류하기 때문입니다.

본 논문에서의 제시하는 cumulative spectral gradient(CSG) c-measure는,

  • lower-dimensional latent space에서 동작하며,
  • pairwise class overlap 정도를 Monte-Carlo 방법으로 추정하여, inter-class similarity matrix를 산출하고,
  • the spectral clustering theory에 따라 K x K Laplacian matrix를 계산한 뒤,
  • the spectrum of the matrix에서 CSG를 계산합니다.

CSG의 장점은,

  • 기존 방법론들보다 빠르고
  • no prior assumption on the dist.
  • class별 분류 난이도에 대한 strong insight를 제공하며
  • CNN에서 잘 동작하고
  • dataset reduction에 쉽게 활용 가능합니다.

2. Previous works

2.1 by Ho and Basu,

그들은 12개의 c-measures를 제안했습니다.

  • F1: Fisher’s Discriminant Ratio
  • F2: inter-class overlap
  • F3: 손쉽게 맞출 수 있는 가장 큰 fraction of points
  • L1/L2/L3: linear separability
  • N1/N2/N3/N4: inter-class overalp을 계산하는 nearest neighbor방식
  • T1: a class를 feature space를 fit 할 수 있는 hyperspheres 갯수
  • T2: (# of total samples) / (data dimensionality)

그러나 small and non-image datasets을 위한 방법이며, two-class problem을 위한 metric입니다. multi-class problem을 위한 연구가 있었지만, 여전히 Large-dataset에는 어울리지 않습니다.

2.2 by Baumgartner and Somorjai

그들은 biomedical and high-dimensional dataset에 적용 가능한 metric을 제안했습니다. 하지만, two-class problem이며 linearly separable하다는 가정이 필요합니다.

2.3 by Duin and Pekalska

dissimilararity matrix를 계산하는 방식을 제안했습니다. 하지만 Euclidean distance를 활용해서 real-world images에 적합하지 않습니다.

2.4 Hub score

본 논문에서처럼 graph 방법론을 썼지만, 계산량이 너무 많습니다.

2.5 by Li

“Intrinsic Dimension”이라는 유일하게 modern image datasets에 적용 가능한 c-measure를 제안했습니다. 하지만 grid-search로 여러 개의 CNN을 학습해야 합니다.

3. Proposed Method

Algorithm Preview

a1

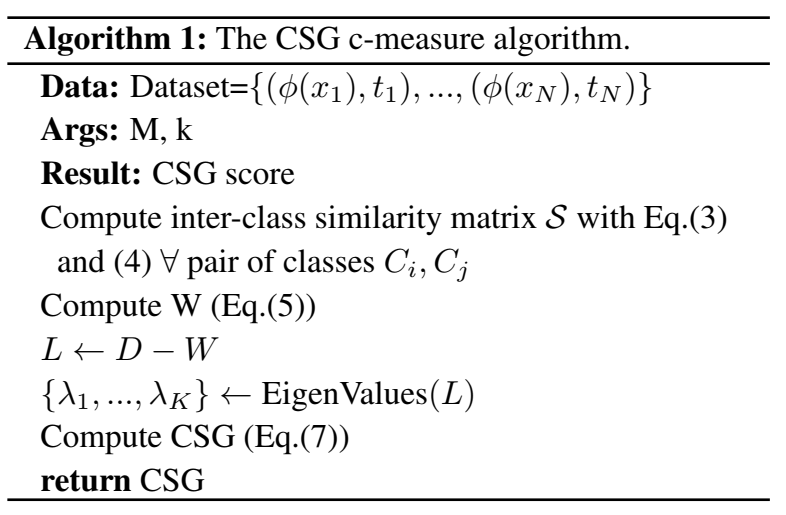
3.1 Class overlap

Class overlap은 본 논문의 핵심이며, 아래와 같이 정의합니다.

  • $x$: input image
  • $\phi$: any function
  • $\phi(x)$: embbeding
\[\int\limits_{\mathbb{R^d}} min(P(\phi(x)|C_i), P(\phi(x)|C_j)) d\phi(x)\]

그런데 위 식은 계산이 너무 어렵습니다. class-overlap은 분포의 유사성과 관련이 높으므로, 계산이 쉬운 KL Divergence 또는 KS test 지표로 대신하기도 합니다. 이런 방법들 중 하나로 the probability product kernel of Jebara et al. 이 있으며 $\rho = 0.5$ 이면 Bhattacharyya kernel이 되고, $\rho = 1$ 이면 inner-product 형태가 됩니다.

\[E_{P(\phi(x)|C_i)} [P(\phi(x)|C_j)] \approx \displaystyle\frac{1}{M} \displaystyle\sum_{m=1}^{M} P(\phi(x_m)|C_j)\]

그런데 $P(\phi(x)|C_j)$에서 prior assumption이 없으므로, K-nearest로 근사합니다.

  • V: hypercube volume k closest samples to $\phi(x)$ in class $C_j$
  • M: total number of samples selected in class $C_j$
  • $K_{C_j}$: number of neighbors around $\phi(x)$ of class $C_j$
\[p(\phi(x)|C_j) = \displaystyle\frac{K_{C_j}}{MV}\]

3.2 Spectral Clustering

이제 similarity matrix $\mathcal{S}$에서 dataset의 complexity를 요약, 지표화 해야합니다. 이를 위해, the spectral clustering theory를 활용합니다.

a1

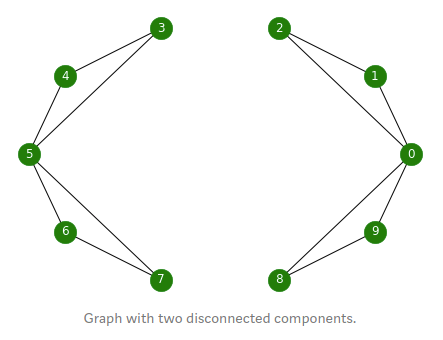
출처: https://towardsdatascience.com/spectral-clustering-aba2640c0d5b

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# Adjacency Matrix final example
A = np.array([
  [0, 1, 1, 0, 0, 1, 0, 0, 1, 1],
  [1, 0, 1, 0, 0, 0, 0, 0, 0, 0],
  [1, 1, 0, 0, 0, 0, 0, 0, 0, 0],
  [0, 0, 0, 0, 1, 1, 0, 0, 0, 0],
  [0, 0, 0, 1, 0, 1, 0, 0, 0, 0],
  [1, 0, 0, 1, 1, 0, 1, 1, 0, 0],
  [0, 0, 0, 0, 0, 1, 0, 1, 0, 0],
  [0, 0, 0, 0, 0, 1, 1, 0, 0, 0],
  [1, 0, 0, 0, 0, 0, 0, 0, 0, 1],
  [1, 0, 0, 0, 0, 0, 0, 0, 1, 0]])

# Degree Matrix
D = np.diag(A.sum(axis=1))
print(D)

# Graph - Laplacian
L = D-A
print(L)

# eigenvalues and eigenvectors of L
vals, vecs = np.linalg.eig(L)
print("num of vals:" + str(vals.shape))
print("num of vecs:" + str(vecs.shape))

# treat samll-number error
vals = np.round(vals+0.000001, 2)
vecs = np.round(vecs+0.000001, 2)

# print results
idx_sorted = np.argsort(vals)
vals_sorted = []
for idx in idx_sorted:
    print("Eigenvalue(", vals[idx], "): Eigenvector:", vecs[:,idx], )
    vals_sorted.append(vals[idx])

# plot the Laplacian spectrum
plt.plot(vals_sorted, 'bo-')
for i, idx in enumerate(idx_sorted):
    plt.annotate(idx, (i-0.1, vals_sorted[i]+0.2))

# 작은 순서대로 4번째까지
interested = vecs[:,[3,5,6]]
interested

# 고유벡터 값들 사이에서 k-means 군집
kmeans = KMeans(n_clusters=4)
kmeans.fit(interested)

# 최종 그룹화 (4개로)
colors = kmeans.labels_
print("Clusters:", colors)

첫 번째 0이 아닌 eigenvalue를 spectral gap이라고 하며, graph의 density를 나타낸다고 합니다. 만약 graph의 모든 노드가 다 연결된 densely connected 상태라면 이 값은 10이 됩니다. 바로 이 두 번째 eigenvalue와 eigenvector를 각각 Fiedler value, Fiedler vector라고 부릅니다. Fiedler value는 graph를 두 개로 나누기 위한 cut 수의 minimum value를 근사합니다. 그리고 Fiedler vector의 부호에 따라 그룹을 분류할 수 있습니다.

  • zero-eigenvalue는 connected components를 의미
  • 0에 가까운 eigenvalue는 거의 두 개로 나누는 components임을 의미
  • 예시에서 두 그룹을 1개의 edge가 연결하기 때문에 eigen-value가 작은 것

Minimum cut method

mincut

출처: https://ratsgo.github.io/machine%20learning/2017/04/27/spectral/

\[MinCut(A, B) = min \frac{1}{4}q^T(D-W)q\]


\[\displaystyle\frac{\partial C}{\partial q} = \displaystyle\frac{\partial [ {\frac{1}{4}q^T(D-W)q-\lambda (q^tq-|V|)]}}{\partial q}=0\]


\[(D-W)q = \lambda q\]

그러므로, $q$는 $(D-W)$ 행렬의 eigenvector

3.3 Inter-class adjacency matrix

Arbitrary Data

  1. Adjacency Matrix 생성: 거리 metric으로 Gaussian이 일반적이라고 함
  2. graph 생성:
    • 거리 threshold
    • k-nearest
    • minimum spanning

This Paper

이미 adjacency matrix로 쓸 수 있는 similarity matrix $\mathcal{S}$를 구했습니다.

  • 쉬운 dataset은 overlap이 적으므로 $\mathcal{S}$의 값이 작음
  • 작은 Laplacian matrix의 spectrum이 작은 eigenvalues로 구성됨

그런데 그런데 $\mathcal{S}$는 Monte-Carlo 근사로 구했으므로, non-symmetric입니다. 그래서 $\mathcal{S}_i$의 각 열을 class i의 signature vector로 인식합니다. 그리고 i와 j가 겹치면 1, 그렇지 않으면 0이 되도록 아래와 같이 Bray-Curtis distance function을 적용합니다.

\[w_{ij} = 1 - \displaystyle\frac{\sum_k |\mathcal{S}_{ik} - \mathcal{S}_{jk}|}{\sum_k |\mathcal{S}_{ik} + \mathcal{S}_{jk}|}\]

3.4 Runtime improvement

Bray-Curtis function & Monte-Carlo mothod를 사용해서 기존 방법들 보다 40배는 더 빠르다고 합니다.

3.5 the CSG complexity measure

a lower eigenvalue spectrum은 a low inter-class overlap을 의미합니다.

f1

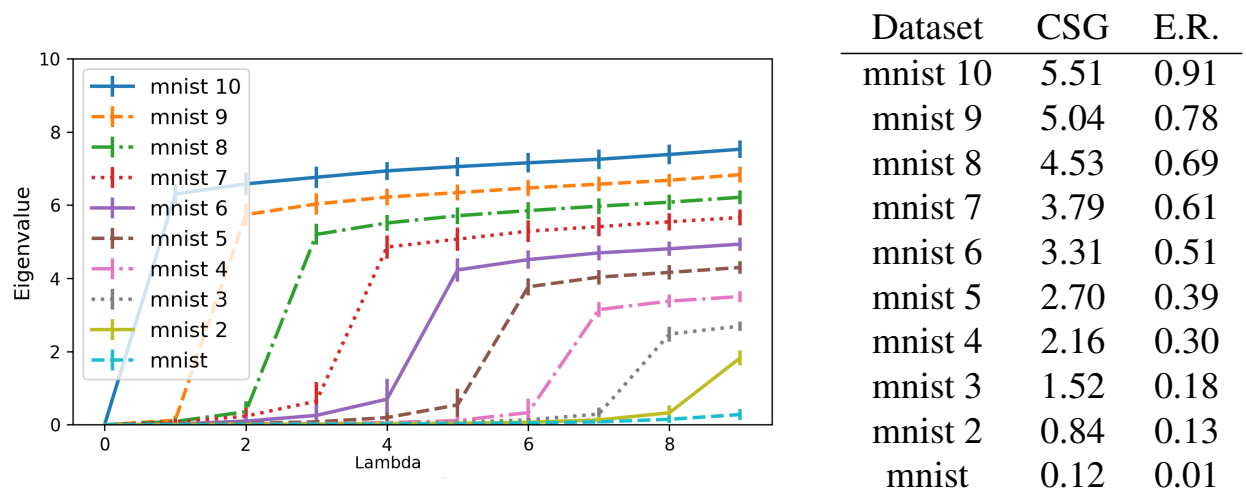
예를들어, 쉬운 dataset인 MNIST의 spectrum은 거의 0에 가깝습니다. 만약 class label를 무작위로 변경하면, dataset의 난이도가 올라가게 되며 eigenvalues의 값도 증가합니다. 또한 more entangled dataset의 경우 더 early step에서부터 eigenvalue가 빠르게 증가 합니다.

  • Overall complexity: the Area Under the Spectrum Curve
  • $CSG = \sum_i cummax(\triangle \widetilde{\lambda})_i$

4. Results

4.1 Embeddings

  1. Raw
  2. t-SNE: to 2D space
  3. CNN$_{AE}$: 9-layer CNN-Autoencoder, trained for 100 epochs
  4. CNN$_{AE}$ t-SNE: t-SNE after CNN$_{AE}$

4.2 Datasets

  • E.R.:AlexNet CNN Error rate
  • K: classes #
  • N: training size

t1

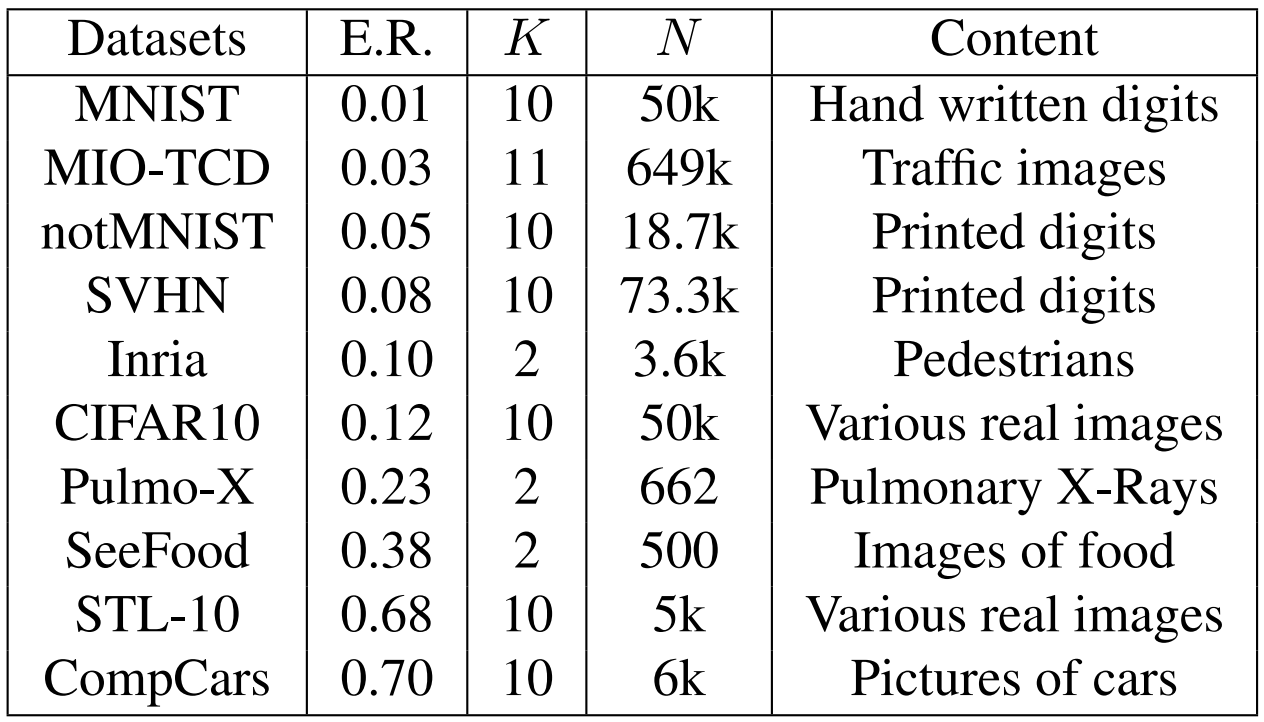
Hyper-parameters

두 개의 HP가 있습니다.

  • M: samples per class for Monte Carlo
  • k: neighbors #

4.3 Experimental results

Comparison with other c-measures

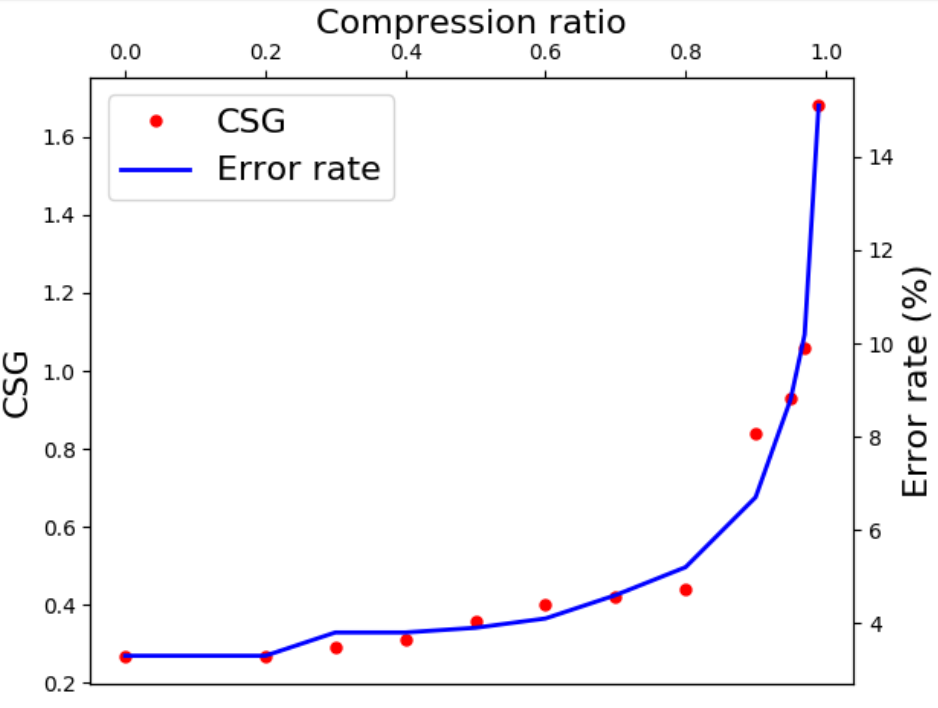
데이터를 조금씩 삭제하면서, CSG가 급격하게 상승하기 전까지 반복합니다.

f3

카테고리:

업데이트:

참고