A Gift from Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning
00. Knowledge Distillation 시초 논문
Knowledge Distillation 개념은 Teacher Network의 성능을 작은 Student Network에 담기위해 고안됐습니다. 처음 논문은 Teacher Network의 softmax 결과를 “soft label”로 정의하고, Student Network가 원래의 hard label과 soft label을 모두 학습하는 방식을 제안했습니다.
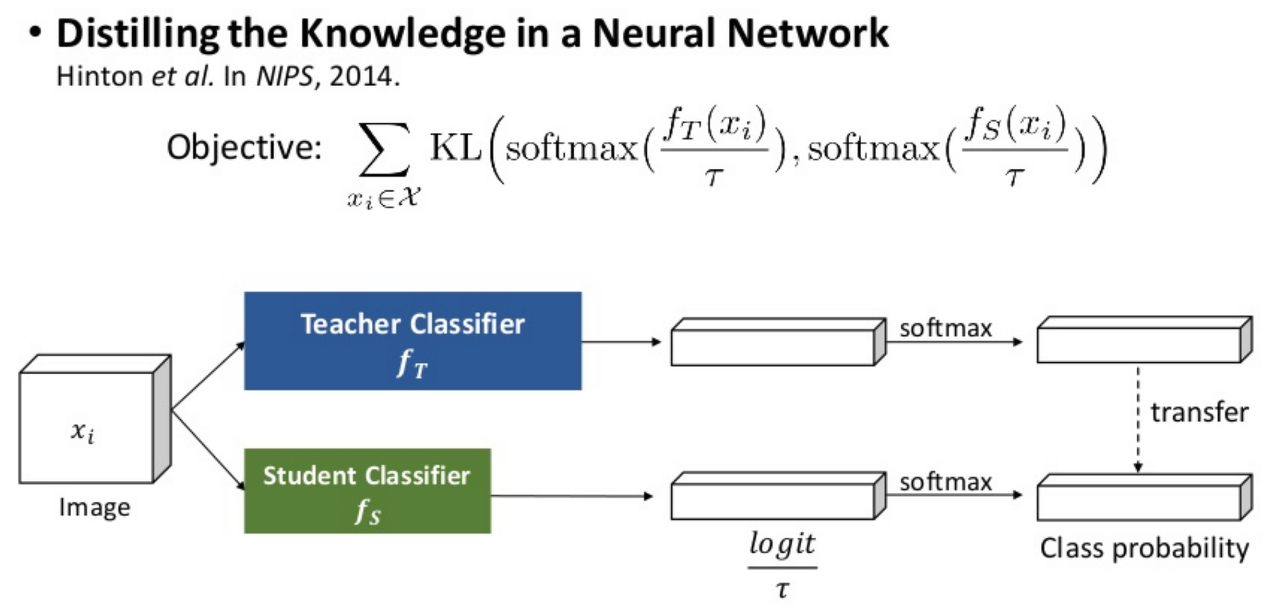
출처: POSTEC 박원표님 https://www.slideshare.net/NaverEngineering/relational-knowledge-distillation
아래에서 review하는 논문은 처음 논문과 최신 논문의 중간 단계입니다. 본 논문에서는 좀 더 효과적인 Knowledge Distillation 방법론을 제안합니다. 본 방법의 장점은 아래와 같다고 합니다.
- Optimized를 훨씬 빠르게 함
- 작은 network에서 성능을 더 향상시킴
- 다른 task에서 학습된 knowledge도 가져올 수 있음
통번역 리뷰는 여기를 참조했습니다.
01. Introduction
KD training이 몇몇 dataset에 대해서 정확도의 향상 달성했지만, very deep network의 optimizing이 어렵다는 문제점이 존재한다고 합니다. Romero[20]는 pretrained teacher의 hint layer와 student의 guided layer를 이용하는 hint-based training 접근방법을 제안했습니다. 하지만, 직접적인 중간 layer를 모방하도록 학습하는 것은 오히려 Student Network의 자유도를 떨어트려 학습을 어렵게 만들 수 있습니다.
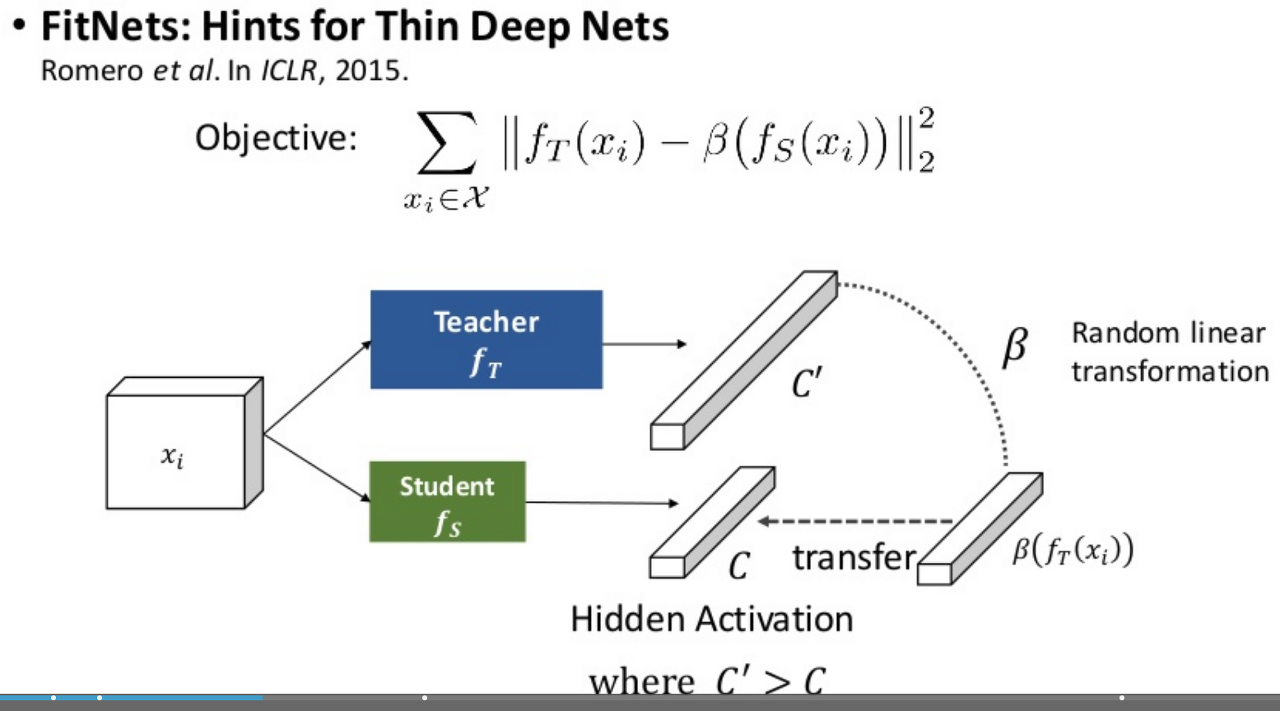
출처: POSTEC 박원표님 https://www.slideshare.net/NaverEngineering/relational-knowledge-distillation
그래서 본 논문에는 아래와 같이 주장합니다.
- Knoledge Distillation 방법론에서는 Knowledge를 어떻게 정의하느냐가 매우 중요
- DNN이 문제해결 process라고 가정할 때, 직접적인 풀이 방법보다는 문제를 푸는 flow를 전달해줘야 한다고 생각
- 문제를 푸는 flow는 DNN에서 layer와 layer 사이의 features에서 얻을 수 있다고 생각
- 그래서 layer와 layer사이의 관계를 정의하기 위해 FSP Matrix를 정의하고, 이를 통해 knowlede를 전달
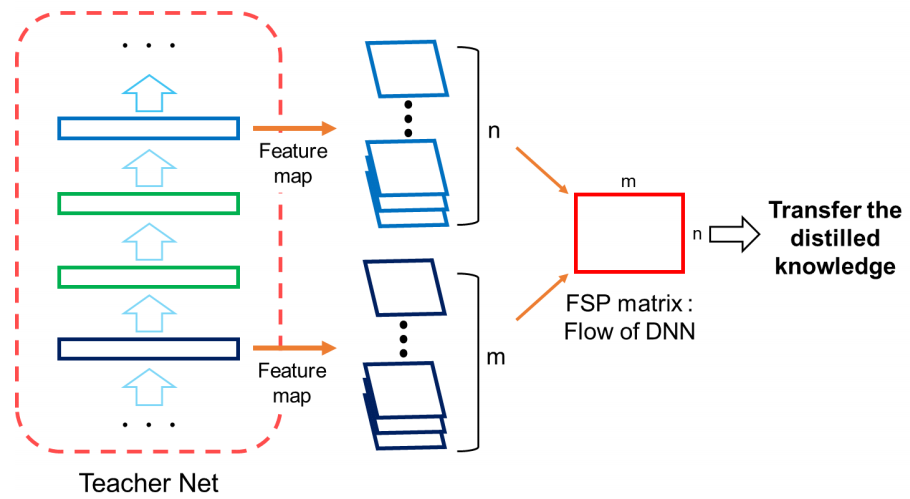
2. Method
앞에서 설명한 것 처럼, layer와 layer 사이의 flow를 담아 Student Network에서 학습을 하도록 하는 것입니다. 중간 flow는 사람에 비유하면, 문제를 푸는 개략적인 방식인 셈입니다. 그렇다고, 선생님과 똑같이만 풀라고 하는 것(Romero[20])은 오히려 부작용을 초래할 수도 있습니다.
그래서 본 논문에서는 FPS matrix $G \in \mathbb{R}^{m \times n}$ 를 아래와 같이 정의합니다. 앞쪽 채널에서 뒤쪽 채널로의 feature간의 inner-product입니다.
$G_{i, j}(x;W) = \displaystyle\sum_{s=1}^h \displaystyle\sum_{t=1}^w \frac{F_{s,t,i}^1(x;W) \times F_{s,t,j}^2(x;W)}{h \times w}$
- $F \in \mathbb{R}^{h \times w \times m}$ : Feature map
- h : height
- w : width
- m : channel
- x : image
- W : weights
이러한 FSP matrix를 Student Network가 배우기 위한 Loss Function은 아래와 같습니다. 가중치를 제외하면 단순한 L2 Loss입니다. 이론적으로는 pair마다 다른 가중치를 줄 수 있지만, 논문에서는 동일한 가중치를 활용했습니다. 전체 architecture 중에서 중요한 부분을 알 수 있다면, 더 높은 가중치를 주는 것도 가능할 것 같습니다.
| $L_{FSP}(W_t, W_s) = \displaystyle\frac{1}{N} \sum_x \sum_{i=1}^n \lambda_i \times | (G_i^T(x;W_t) - G_i^S(x;W_s) | _2^2$ |
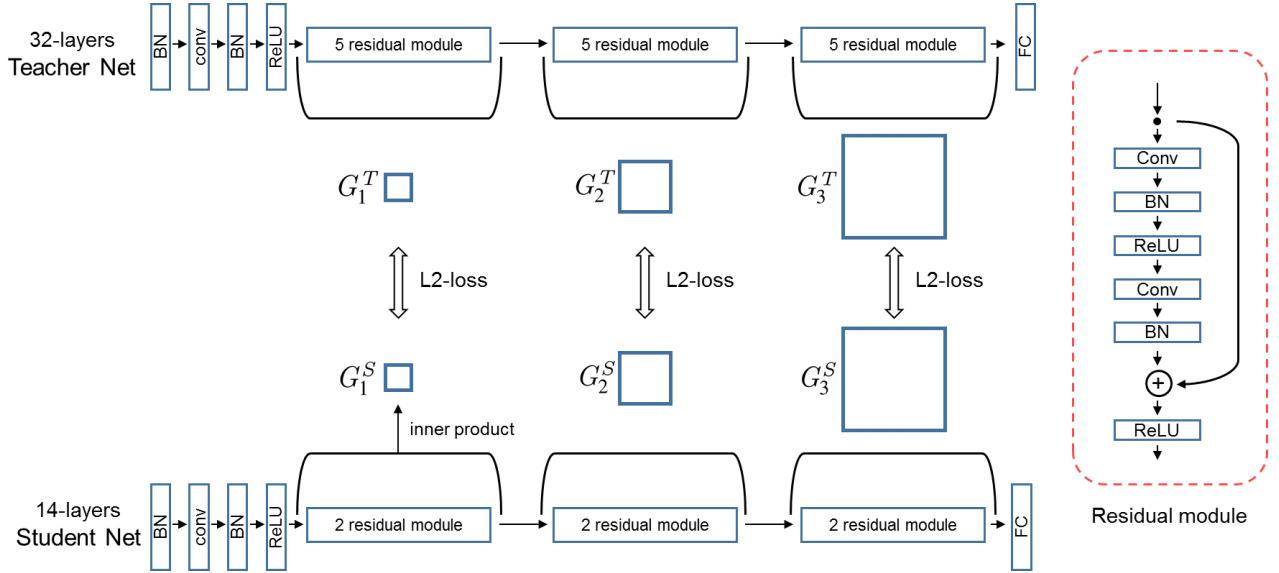
학습 과정도 매우 간단합니다. 먼저 FSP matrix를 학습하여 전체 가중치를 update합니다. 그 후, 원래 task에 대해 학습하기만 하면 됩니다!

3. Experiment
저자들은 먼저 동일한 Network Size에서 Optimization 속도 및 성능을 측정했습니다. CIFAR-10에서의 결과는 다음과 같습니다.
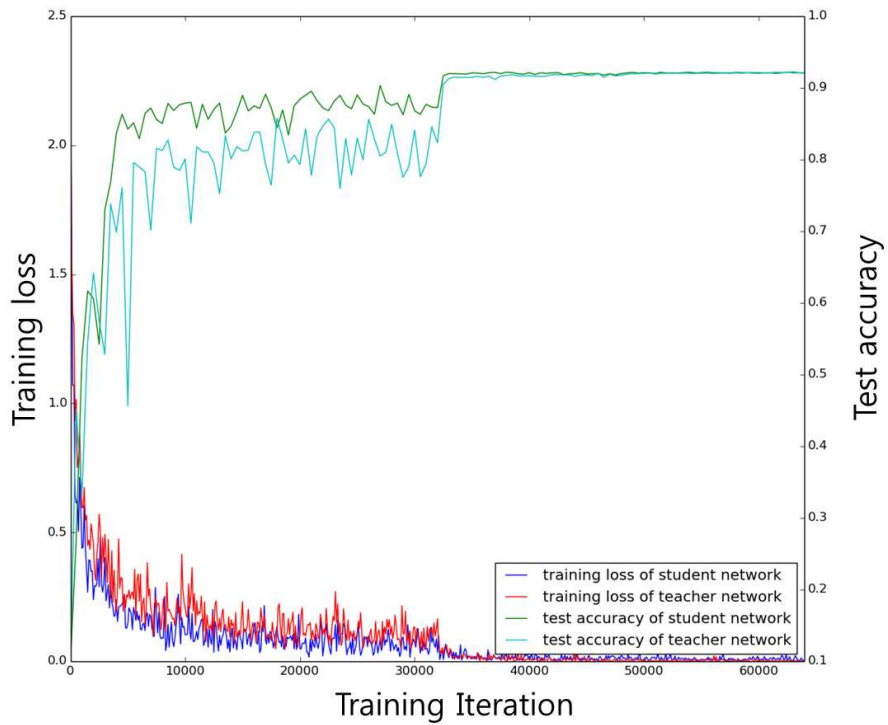
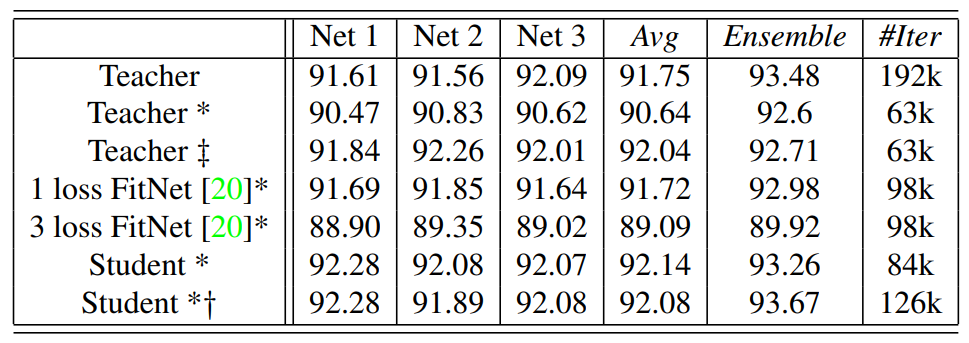
original은 총 64,000 iters 학습합니다. *의 의미는 1/3만큼만(21,000 iters) 학습했다는 뜻입니다. Student*는 Stage1에서 21,000 iters 그리고 Staget2에서 network 각각에 대해 21,000 iters x 3, 그래서 총 84,000 iters를 학습했습니다. ++ 네트워크는 original에서 추가로 21,000 학습합니다. *+ 네트워크는 FSP를 무작위로 섞어서 Stage1을 학습습니다.
- Teacher*와 Student*를 비교해보면, 동일한 iterations에서 제안한 방법의 성능이 더 좋습니다.
- Teacher++와 Student*를 비교해보면, 단순한 fine tuning보다 Knowledge Distillation이 더 효율적입니다.
- FitNet*과 Student*를 비교하면, 본 논문이 제안한 방법의 성능이 더 좋습니다.
- 중간 feature를 바로 전달하는 것보다, flow를 전달하는 것이 효율적
- FitNet1이 FitNet3보다 성능이 더 좋습니다.
- 중간 feature를 너무 많이 따라하게 하는 것은, 과도한 제약사항
- 동일한 init에서 학습하기 시작하므로 Student*의 앙상블 향상 효과가 크지 않음
- FSP matrix permute 연산을 통해 init. point를 다르게 하면 앙상블 효과가 커짐
Teacher보다 작은 size의 Student 모형을 학습할 때도 본 논문에서 제시하는 방법의 성능이 더 좋음을 확인했다고 합니다.

ImageNet에서 학습된 모형으로 CUB-200 Dataset에 적용할 때도, 본 논문에서 제안한 방법의 성능이 가장 좋다고 합니다. 일반적인 Transfer Learning의 효과가 비교되지 않는 점의 의아하긴 합니다.

