jaehwi

I am an amazing person!

8 분 소요

1. Introduction

Deep Ensemble (DE)[Lakshminarayanan et al., 2017]는 간단한 앙상블 방법이다. 동일한 모형을 random seed만 바꿔서 여러 번 학습하면 되기 때문이다. 그런데도 다양한 tasks에서 좋은 성능을 보여주고 있다. 몇몇 연구들은 DE의 효과성을 밝혀내려 했다. 그 중 한 이론은 DE가 Bayesian Model Average (BMA) 프로세스의 근사라는 것이다. 그런데 가장 복잡한 Bayesian inference 알고리즘들도 DE만큼의 파라미터 탐색력을 보여주지 못했다.

DE는 학습하기 쉽지만, inference 시간 및 메모리 관리가 어렵다. 이를 해결하기 위한 방법 중 하나가 Knowledge Distillation (KD) 이다. Student 모형은 Teacher 모형의 결과를 모방하며 학습한다. DE teacher 모형들을 한 개의 student 모형이 따라하는 연구들도 있었지만, 다수의 subnetworks로 구성된 student 모형을 학습하는 것이 더 효과적인 것으로 확인됐다. 그럼에도 불구하고 KD 모형들의 성능은 DE 보다 크게 떨어졌다.

성능 하락이 원인은 다양하겠지만, 이번에 제기하는 가장 핵심 문제는 기존 KD가 효과적으로 DE teacher의 다양성을 전달하지 못한다는 것이다. 이미지 분류 task를 가정해보자. 학습 시에는 Figure 1과 같이 거의 완벽한 결과를 보여준다. 이런 상황에서 학습 데이터를 다시 사용하는 것은 예측 다양성 측면에서 그다지 도움이 되지 않는다. 이는 DE가 예측 다양성을 잘 확보한 것과 상반되는 모습이다.

f1

그래서 본 논문에서는 student 모형의 다양성을 강화할 수 있는 방법을 제안한다. 아이디어는 간단한데, 동일한 학습 데이터셋을 사용하는 대신 pertubed 데이터셋을 사용하여 다양성이 증가하도록 만드는 것이다. 이를 위해 Output Diversified Sampling (ODS, Tashiro et al., 2020) 방법론을 활용했다. ODS는 결과는 크게 바꾸는 작은 input 변화를 찾는 샘플링 방법이다. 

ODS를 통해 변경된 inputs 들은 DE teacher 모형의 결과값의 다양성을 크게 증가시키는 것을 실험적으로 확인했다. 추가로 ODS 변화의 역할을 분석함으로써 새롭게 제안하는 방법론의 의의를 설명했다. 특히 우리의 방법론은 Jacobian matching procedure를 근사하는 것으로 해석될 수 있다. 

2. Backgrounds

2.1 Settings and notations

본 논문에서는 K개 라벨의 분류 문제를 다룬다.

  • student 모형은 $\mathcal{S}(x)$
  • teacher 모형은 $\mathcal{T}(x)$
  • logits before softmax는 $\hat{\mathcal{S}}(x)$, $\hat{\mathcal{T}}(x)$
  • k번째 output은 $\mathcal{S}^{(k)}(x)$
  • j번째 ensemble memeber DE 모델은 $\mathcal{T}_{j}(x)$
  • j번째 subnetwork는 $\mathcal{S}_{j}(x)$

2.2 Knowledge distillation

KD는 $\mathcal{S}(x)$가 $\mathcal{T}(x)$와 동일한 output을 생성하도록 학습하는 것이다. 그래서 기본 cross-entropy loss에 추가로 $\mathcal{S}(x)$, $\mathcal{T}(x)$ 결과값들 간의 KL-divergence를 loss로 사용한다.

2.3 BatchEnsemble and one-to-one distillation

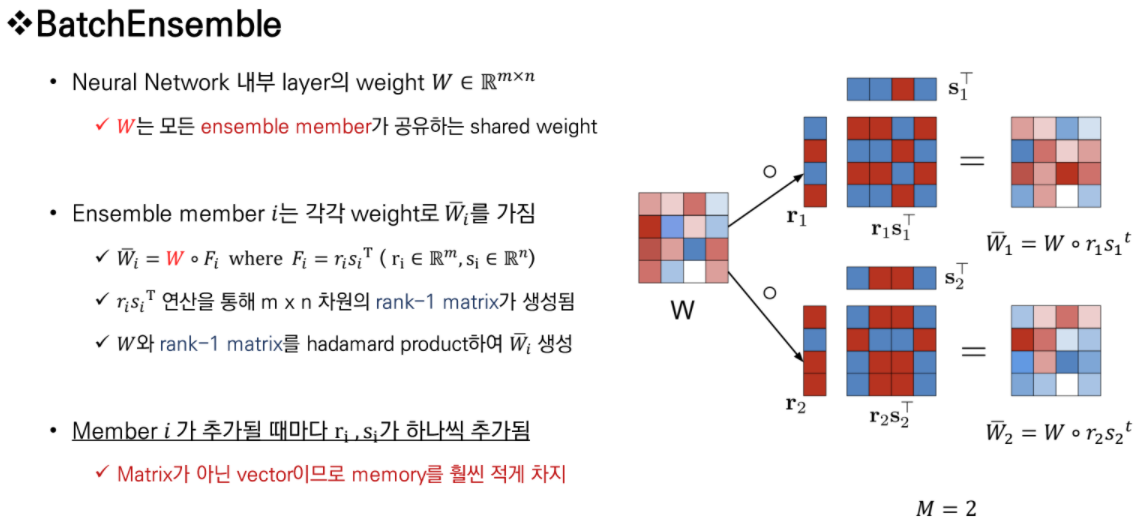
BatchEnsemble (BE) [Wen et al., 2020] 은 경량화된 ensemble 방법으로, weight-sharing을 통해 파라미터 수를 줄인다. 특히 각각의 BE layer들은 아래 이미지와 같이 공유되는 weights W와, rank-one factors $r_j s_j^{\top}$로 구성된다. 즉, j번째 subnetwork는 $W \circ r_j s_j^{\top}$ 이렇게 계산되며, 결과적으로 BE는 파라미터 수가 매우 크게 감소한다.

be

출처: [고려대학교 산업경영공학부 DSBA 연구실](https://www.youtube.com/watch?v=Gt6JH1mH2WI)


Mariet et al. [2020]은 BE의 개선을 위해 모두 학습된 DE teacher 모형에서 distillation을 진행했다. distillation을 진행하며, $\mathcal{S}_{j}(x)$는 $\mathcal{T}_{j}(x)$의 결과로 학습한다. 이것을 one-to-one distillation framework로 부르겠다.

f2

2.4 Output diversified sampling (ODS)

ODS는 주어진 함수 결과들의 다양성을 최대화하는 샘플링 방법이다. 원래는 adversarial attack의 성능을 올리기 위한 random input perturbation을 생성하기 위해 고안됐다. ODS는 input space에서 randomly sampled vector $\mathcal{w}$와 함수 결과와의 유사도를 극대화하는 방향을 찾는다. 그러한 방향을 따라가면 w의 임의성 때문에 output이 더욱 다양해질 수 있다.

f3

3. Learning from Ensembles with Output Diversification

3.1 One-to-one distillation with ODS

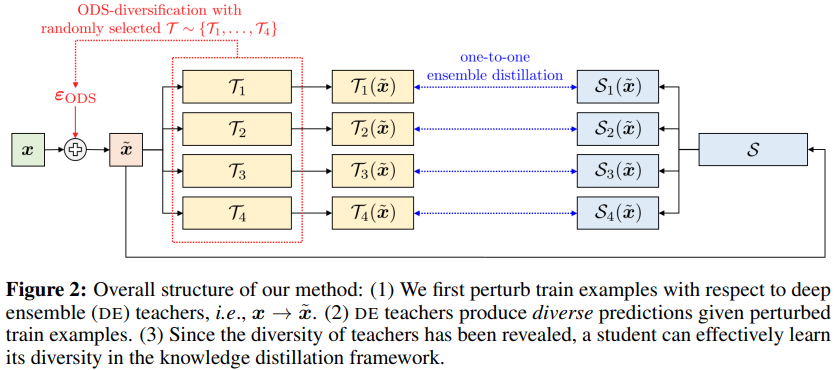
teacher 모형의 다양성 확보를 위해 다음과 같이 diltillation에 ODS를 적용하는 것을 제안한다.

\[\tilde{x} = x + \eta\varepsilon_{ODS}(x, softmax(\hat{\mathcal{T}}_r(x) / \tau), w)\]

이상적으로는 M개의 ODS vectors를 계산해야 하지만, gradient 계산량이 너무 많아진다. 그래서 그 대신 1개의 teacher 모델을 고르고, input perturbation을 생성한다. 생성된 input perturbation은 모든 students에서 사용한다.

fo5

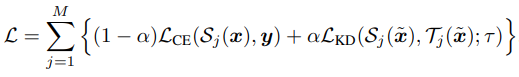
여기에서 활용한 주요 가정은 특정 teacher에서 생성한 diversity direction을 다른 teachers에도 사용 가능하다는 것이다. 즉 아래와 같이 임의의 teacher에서 생성한 perturtions은 다른 teacher에서의 또 다른 임의의 vector에 의한 perturbation으로 근사된다.

fo6

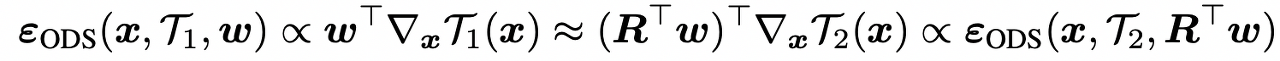
마지막으로 high confidence인 포인트에서는 더욱 변화를 크게 주기 위해 $C_{max}(x, \mathcal{T}_r(x), \tau)$ term을 추가하여 ConfODS를 아래와 같이 정의한다.

\[\tilde{x} = x + \eta C_{max}(x, \mathcal{T}_r(x), \tau) \varepsilon_{ODS}(x, softmax(\hat{\mathcal{T}}_r(x) / \tau), w)\]

학습 과정은 다음과 같다.

a1

3.2 Interpretation as approximate Jacobian matching

이전 연구들에서 작은 노이즈의 input을 사용한 KD는 teacher와 student의 jacobian을 맞추는 역할을 한다는 것을 확인할 수 있었다. 1차 테일러 급수 정리를 활용하면 noised input을 활용한 KD loss는 아래와 같이 정리할 수 있다.

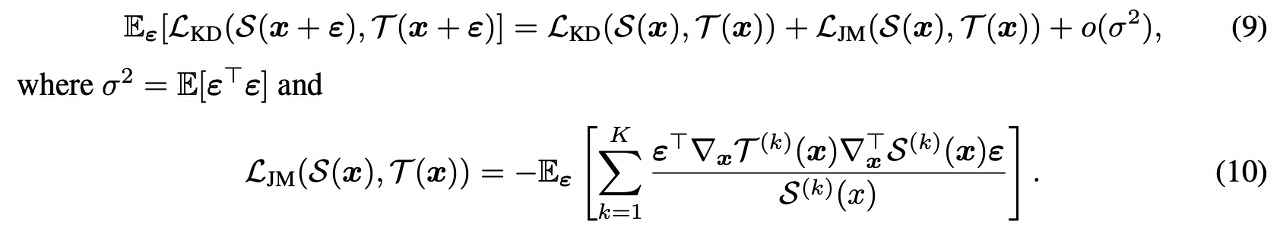
fo9_10

5. Experiments

5.1 Experimental setup

Datasets & Networks

  • ResNet-32 for CIFAR-10
  • WideResNet-28x10 for CIFAR-100 and TinyImageNet

Hyperparameters

  • stay consistent with the convention of (α, τ ) = (0.9, 4) for all methods
  • For CIFAR-100 and TinyImageNet, we used the value (α, τ ) = (0.9, 1) for all methods
  • ODS step-size η to 1/255 across all settings

Uncertainty metrics

  • Accuracy (ACC)
  • Negative Log-Likelihood (NLL)
  • Expected Calibration Error (ECE)
  • Brier Score (BS)
  • Deep Ensemble Equivalent (DEE) score

5.2 Impact of ODS on diversities

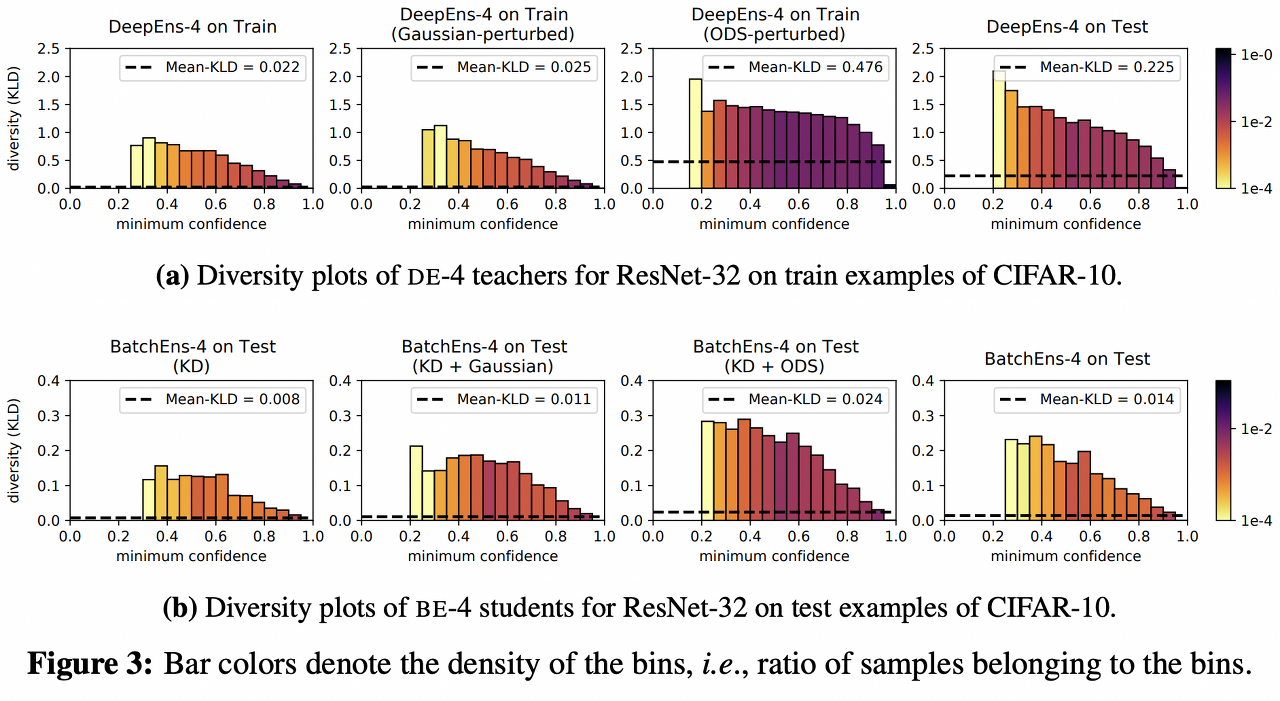
ODS perturbation를 통한 diversities 효과를 확인하기 위해 Figure 3의 그래프를 생성했다. 이를 위해 먼저 target models의 결과들을 수집하고, confidence에 따라 binning. bin 마다 ensemble members 결과들 간 average pairwise KL-divergence 계산했다. 또한 bin counts로 가중치를 부여하여 대표값을 생성했다.

  • Fig. 3a를 보면 가중치가 높은 구간에서는 diversity가 낮게 측정된다.
  • the mean-KLD 값도 train-test 간의 차이를 확인할 수 있다. (3a 1번 vs 4번)
  • Gaussian perturbation도 별반 차이가 없다. (3a 2번)
  • ODS는 굉장히 크게 diversity를 증가시킨다. (3a 3번)
  • BE 결과를 비교한 Fig. 3b에서도 ODS를 사용한 3번 그래프가 상대적으로 diversity가 높다.

f3

또한 임의의 teacher에서 생성한 ODS를 다른 teacher에서 쓸 수 있다 정리한 것처럼, 외부 ODS를 썼을 때의 diversity 그래프는 다음과 같다. 일반 DE의 diversity보다 더 큰 것을 확인할 수 있다.

f6

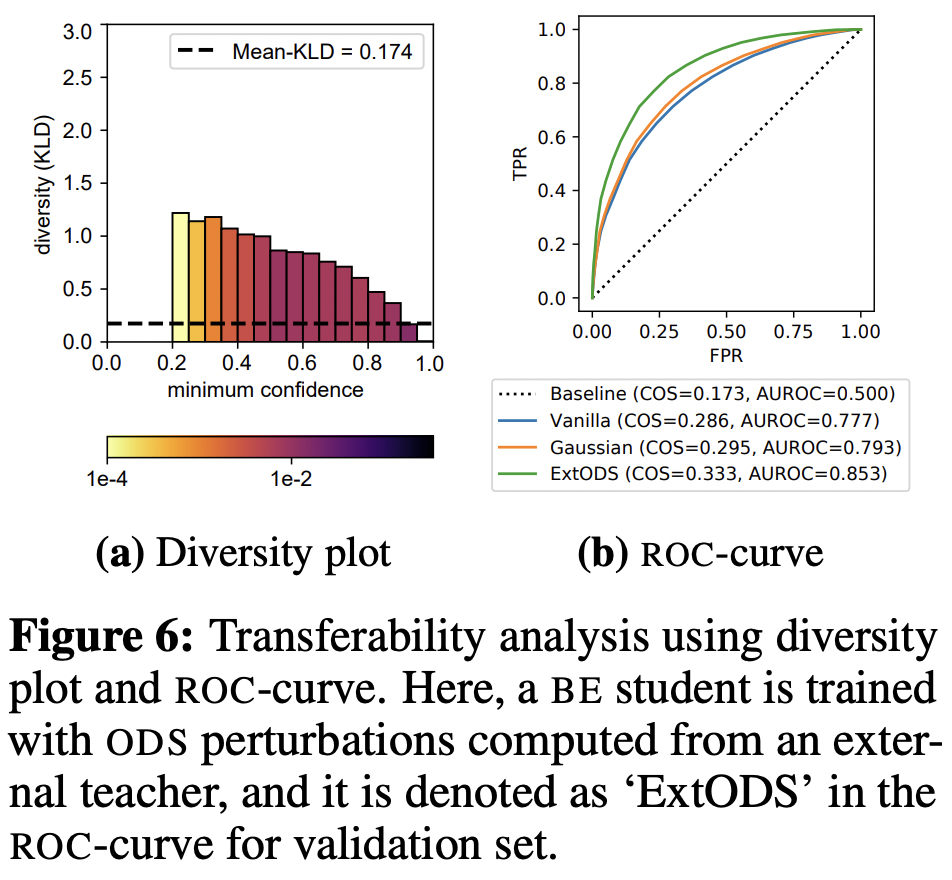
5.3 ODS for Jacobian matching

skip :)

5.4 Main results: image classification tasks

t1

t2

참고