jaehwi

I am an amazing person!

3 분 소요

00. 개요

가용 변수가 너무 많은 경우 데이터분석 패키지들을 이용해 데이터 차원축소를 진행합니다. 데이터 차원축소는 두 가지 방법이 있습니다. 먼저 변수선택을 통해 차원을 축소할 수 있고, 또 다른 방법은 더 작은 차원으로 특성들을 이동하는 것입니다.

※ 참고

데이터의 차원을 너무 어렵게 생각하지 말고, 분석할 데이터 항목의 숫자로 생각하면 간단하다!

01. PCA (주성분분석)

n차원의 데이터 공간에서 가장 분산이 큰 방향의 k차원으로 이동(mapping)합니다(단, n>k). 분산이 큰 방향은 데이터의 scale에 민감하므로, PCA를 적용하기 전 표준화 작업이 선행돼야 합니다. 

PCA의 pseudo code는 아래와 같습니다.

  1. 원본 데이터를 표준화합니다.
  2. 표준화 또는 정규화된 데이터의 공분산 행렬을 생성합니다.
  3. 공분산 행렬에서 고유 벡터(eigenvector)와 고윳값(eigenvalue)을 계산합니다.
  4. 고윳값의 내림 정렬 기준으로 고유 벡터를 정렬합니다.
  5. 최상위 k개의 고유벡터를 선택합니다.

python 코드를 활용하여 고유벡터를 구해봅니다.

from sklearn.preprocessing import StandardScaler
import numpy as np

# 1.표준화
sc = StandardScaler()
train_n = sc.fit_transform(train)

# 2.공분산 행렬
covm = np.cov(train_n.T)

# 3.고유벡터 & 고윳값
evl, evt = np.linalg.eig(covm)

sklearn의 PCA클래스를 이용하면 간편합니다!

# 2차원으로 축소
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
train_n = pca.fit_transform(train)

# 원래 차원의 모든 주성분 파악
pca = PCA(n_components=None)
train_n = pca.fit_transform(train)
pca.explained_variance.ratio_

02. LDA(선형 판별 분석)

LDA도 PCA와 유사한 방법론입니다. 그러나 PCA는 비지도학습 계열이지만, LDA는 Target에 대한 정보가 필요한 지도학습 계열에 속합니다. 

LDA는 두 가지 가정이 필요합니다. 하지만, 아래의 가정이 조금 위반되더라도 차원 축소를 상당히 잘 해낸다고 합니다. - 각 클래스의 데이터는 정규분포를 따른다. - 클래스가 동일한 공분산 행렬을 가지고 샘플은 서로 독립이다.

LDA의 pseudo code는 아래와 같습니다.

  1. feature d개를 가진 원본 데이터를 표준화합니다.
  2. 각 클래스에 대해 d차원의 평균 벡터를 계산합니다.
  3. 클래스 간의 산포 행렬 $\mathcal{S}_B$와 클래스 내 산포 행렬 $\mathcal{S}_W$를 계산합니다.
  4. $\mathcal{S}_W^{-1} \mathcal{S}_B$ 행렬로 PCA를 수행합니다.

클래스 별 분류를 잘 수행하기 위해서는, 클래스간 평균이 멀고 동시에 각 클래스의 분산이 작아야 합니다. 그렇기 떄문에 클래스 간, 그리고 클래스 내 산포행렬을 구하는 것입니다.
*참고: LDA 설명이 훌륭한 블로그

sklearn의 LDA 클래스를 이용하면 손쉽게 처리가 가능합니다.

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)
train_n = lda.fit_transform(train, target)

03. kernel PCA

주어진 데이터에서 바로 차원을 축소하면 분류가 쉽지 않은 경우가 발생합니다. 아래와 같은 비선형 케이스들이 이에 해당합니다. 이러한 비선형 케이스들은 먼저 고차원으로 mapping 한 이후, 분류를 할 수 있는 차원으로 변형하여 다시 차원을 축소해야 합니다.

PCA

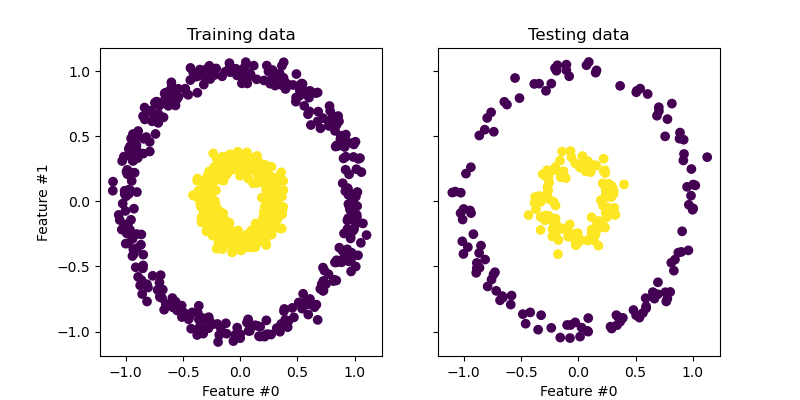
*출처: 구글 “kernel PCA” 이미지검색

많이 활용되는 kernel들은 다음과 같습니다. - 다항 커널 - 시그모이드 커널 - 가우시안 커널

sklearn을 활용하면 kernel PCA를 손쉽게 수행할 수 있습니다.

from sklearn.decomposition import KernelPCA
kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
train_n = kpca.fit_transform(train)

참고